티스토리 뷰

강의 서쪽에 N개의 사이트가 있고 강의 동쪽에 M개의 사이트가 있을 때 다리를 최대한 많이 놓을 수 있는 경우의 수를 구하는 문제
문제
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
출력
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.
풀이

이 문제 또한 점화식을 세워서 메모이제이션을 하며 풀어야 하니까 DP 배열을 선언한 후 0으로 초기화 합니다. 저는 DP[N][M] = 서쪽에 N개의 사이트가 있고 동쪽에 M개의 사이트가 있을 때 다리를 놓을 수 있는 경우의 수로 정의 하였습니다. 이제 N = 1 부터 테이블을 채워 봅시다.
예제의 첫번째 케이스를 보면 N과 M이 같을 때엔 경우의 수가 항상 1이라는 것을 알 수 있습니다. 이 경우엔 계산할 필요 없이 바로 1을 출력하면 됩니다.

그리고 두번째 케이스를 보면 N이 1일 때엔 M에 따라 경우의 수가 늘어납니다.

그러면 앞날은 몰라도 일단 N이 1일 때엔 모든 경우의 수를 예측할 수 있고 이것을 기저 조건으로 설정 할 수 있습니다.
이제 N = 2 부터 테이블을 채워야 하는데 아직은 규칙을 찾기 힘드니까 N = 2 / M = 3 일 때 다리를 놓을 수 있는 경우의 수를 생각해 봅시다.
 |
 |
 |
N = 2 / M = 3 일 때 놓을 수 있는 경우의 수는 위와 같이 3가지가 있습니다.
 |
 |
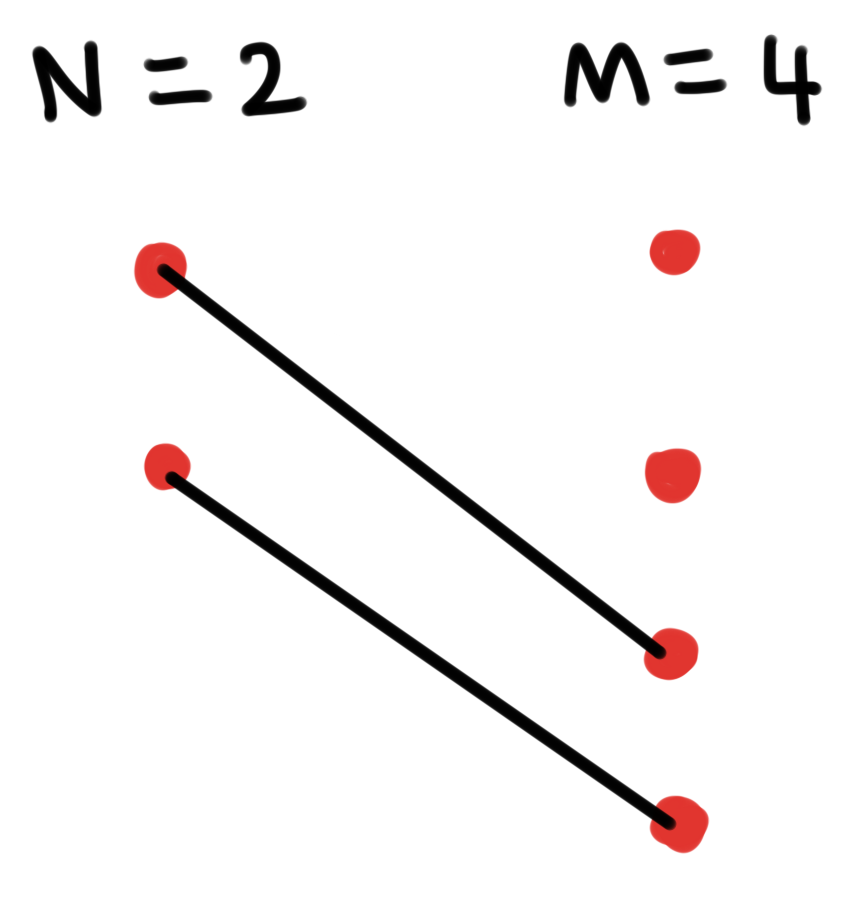 |
그리고 N = 2 / M = 4 일 때엔 N = 2 / M = 3 경우에 위 3가지를 더한 6가지 경우가 있습니다. 그러면 다음과 같이 테이블을 채울 수 있습니다.
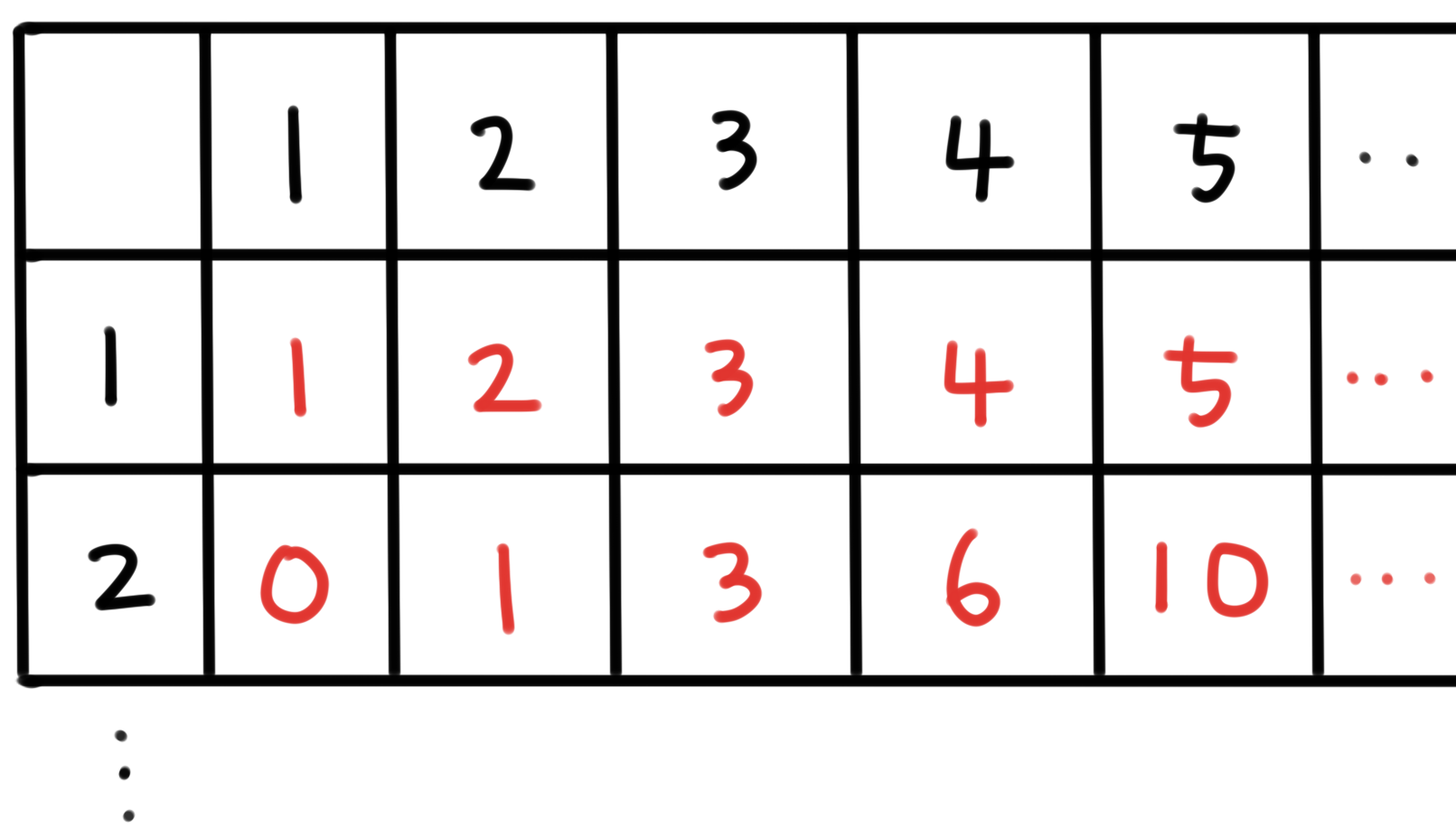
그러면 뭔가 규칙이 보일 것입니다.
DP[2][2] = DP[1][1] + DP[2][1]
DP[2][3] = DP[1][2] + DP[2][2]
DP[2][4] = DP[1][3] + DP[2][3] ... 이 됩니다.
우리는 여기에서 DP[N][M] = DP[N-1][M-1] + DP[N][M-1] 이라는 점화식을 이끌어 낼 수 있습니다. 이것을 코드로 작성하면 됩니다.
코드
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int T;
cin >> T;
for (int i = 0; T > i; i++)
{
int west, east;
cin >> west >> east;
//양 쪽 갯수가 같으면 계산할 필요 없으니까 바로 출력
if (west == east)
{
cout << 1 << "\n";
continue;
}
//DP[west][east] = 서쪽에 west개의 사이트가 있고 동쪽에 east개의 사이트가 있을 때 다리를 놓을 수 있는 경우의 수
vector<vector<long long>> DP(west + 1, vector<long long>(east + 1, 0));
for (int j = 1; east >= j; j++)
DP[1][j] = DP[1][j-1] + 1; //기저 조건 설정
for (int j = 2; west >= j; j++)
{
for (int k = j; east >= k; k++)
DP[j][k] = DP[j-1][k-1] + DP[j][k-1];
}
cout << DP[west][east] << "\n";
}
return 0;
}'알고리즘 문제 풀이 > DP' 카테고리의 다른 글
| [C++] 백준 온라인 저지 1904번 01타일 풀이 (0) | 2021.11.27 |
|---|---|
| [C++] 백준 온라인 저지 11052번 카드 구매하기 풀이 (0) | 2021.11.25 |
| [C++] 백준 온라인 저지 9461번 파도반 수열 풀이 (0) | 2021.11.20 |
| [C++] 백준 온라인 저지 11727번 2 x n 타일링 2 풀이 (0) | 2021.11.19 |
| [C++] 백준 온라인 저지 2193번 이친수 풀이 (0) | 2021.11.18 |
- Total
- Today
- Yesterday
- hackerrank
- c++
- 컴퓨터공부
- 깊이우선탐색
- c언어
- 프로그래밍
- 기초
- 캐나다생활
- 애플
- greedy
- BFS
- 해커랭크
- DFS
- 문제풀이
- 컴퓨터사이언스
- 영어공부
- 알고리즘
- 캐나다
- 그리디
- 코딩공부
- 컴퓨터
- C언어기초
- 스위프트플레이그라운드
- 프로그래머스
- 하드웨어
- 다이나믹프로그래밍
- 너비우선탐색
- 백준
- dp
- 아이패드
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
