티스토리 뷰

나선 모양으로 뻗어져 나가는 정삼각형들 중 N번째 정삼각형의 변의 길이를 구하는 문제
문제
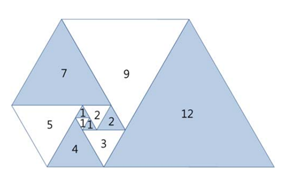
위 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
풀이

이 문제는 비교적 쉽게 그림에 답이 나와 있어서 그림대로 점화식을 세워서 풀었습니다. 그림에서 6번째 삼각형의 변의 길이는 3이고 이것은 첫번째 삼각형의 변의 길이 1과 5번째 삼각형의 변의 길이 2를 합친 길이입니다. 그 다음 7번째 삼각형은 2번째 삼각형과 6번째 삼각형의 변의 길이를 합친 것이구요.
그러면 DP 배열의 i번째 원소를 i번째 삼각형의 변의 길이라고 가정 한다면 DP[i] = DP[i-5] + DP[i-1] 이라는 점화식을 세울 수 있습니다. 100번째 원소는 값이 아주 커지니까 DP 배열의 자료형은 long long으로 선언하는 것을 잊지 마세용~
코드
#include <iostream>
#include <vector>
using namespace std;
const int MAX = 100;
int main()
{
int T;
cin >> T;
vector<long long> DP(MAX + 1, 0); //DP[i] = i번째 나선에 있는 정삼각형 변의 길이
DP[1] = 1;
DP[2] = 1;
DP[3] = 1;
DP[4] = 2;
DP[5] = 2;
for (int i = 6; MAX >= i; i++)
DP[i] = DP[i-5] + DP[i-1];
for (int i = 0; T > i; i++)
{
int N;
cin >> N;
cout << DP[N] << "\n";
}
return 0;
}'알고리즘 문제 풀이 > DP' 카테고리의 다른 글
| [C++] 백준 온라인 저지 11052번 카드 구매하기 풀이 (0) | 2021.11.25 |
|---|---|
| [C++] 백준 온라인 저지 1010번 다리 놓기 풀이 (0) | 2021.11.20 |
| [C++] 백준 온라인 저지 11727번 2 x n 타일링 2 풀이 (0) | 2021.11.19 |
| [C++] 백준 온라인 저지 2193번 이친수 풀이 (0) | 2021.11.18 |
| [C++] 백준 온라인 저지 10844번 쉬운 계단 수 풀이 (0) | 2021.11.17 |
- Total
- Today
- Yesterday
- 스위프트플레이그라운드
- 프로그래머스
- 그리디
- greedy
- C언어기초
- 깊이우선탐색
- 영어공부
- 너비우선탐색
- dp
- 컴퓨터
- 애플
- 문제풀이
- 기초
- 코딩공부
- 하드웨어
- c언어
- DFS
- 컴퓨터사이언스
- 컴퓨터공부
- 프로그래밍
- 해커랭크
- BFS
- 캐나다
- hackerrank
- 알고리즘
- 백준
- 캐나다생활
- c++
- 아이패드
- 다이나믹프로그래밍
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
