티스토리 뷰

주어진 그래프가 이분 그래프인지 아닌지 판별하는 문제
문제의 조건
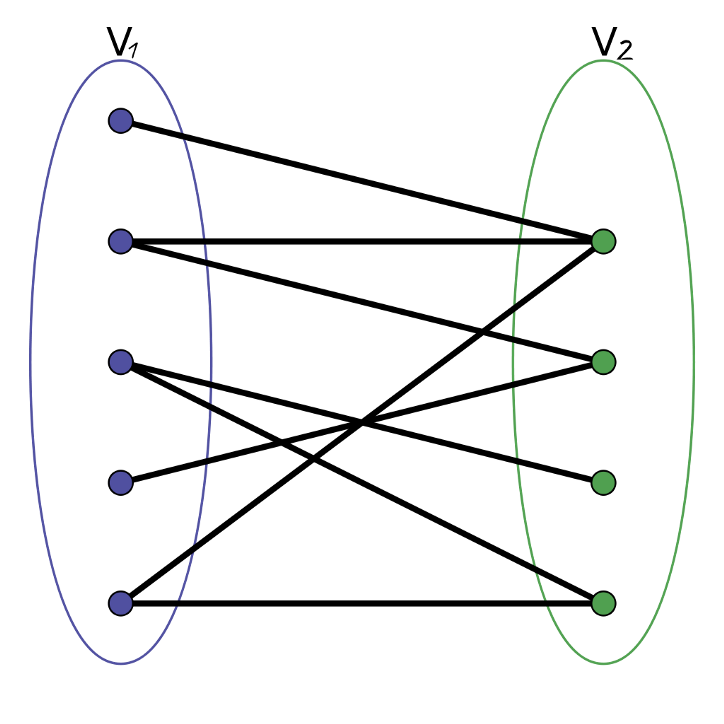
그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.
출력
K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.
풀이 과정
알고리즘을 공부하고 있는 책(코딩 테스트를 위한 자료 구조와 알고리즘 with C++)에 있는 이분 그래프 판별 알고리즘으로 풀었는데 틀렸어요.
휴... 이 책이 최신 c++ 문법 배우기엔 좋은데 알고리즘은 조금씩 엉성한 느낌...
암튼 그래서 구글링으로 좀 더 보완한 후에 통과할 수 있었습니다.
1. 양방향 그래프를 만든다.
2. 이분 그래프를 판별하려면 각 노드에 색칠을 해 줘야 함. 색칠용 enum class를 만든다.
3. 이분 그래프 판별을 위한 색칠을 할 때 현재 노드와 연결된 노드는 현재 노드와 다른 색으로 색칠해야 한다. <= 이것이 제일 중요!
4. DFS로 그래프를 탐색하면서 아직 방문하지 않은 노드라면 색칠한다.
5. 전체 그래프를 검사하는 함수를 만들어서 DFS가 끝난 후 연결된 노드끼리 서로 다른 색으로 칠해져 있는지 확인한다.
모두 다른 색으로 칠해져 있다면 true -> 이분 그래프니까 YES 출력
서로 연결된 한 쌍의 노드라도 같은 색으로 칠해져 있다면 false -> 이분 그래프가 아니니까 NO 출력.
코드
#include <iostream>
#include <vector>
#include <string>
using namespace std;
//노드 색칠용 컬러
enum class COLORS
{
NONE,
RED,
BLACK
};
COLORS curColor = COLORS::RED;
vector<pair<bool, COLORS>> visited;
void dfs(vector<vector<int>>& graph, int cur)
{
for (int i = 0; graph[cur].size() > i; i++)
{
auto next = graph[cur][i];
if (!visited[next].first)
{
//연결된 노드가 아직 방문하지 않은 정점이면 현재 노드와 다른 색으로 칠한다.
if (COLORS::RED == visited[cur].second) curColor = COLORS::BLACK;
else curColor = COLORS::RED;
visited[next] = make_pair(true, curColor);
dfs(graph, next);
}
}
}
bool isBipartiteGraph(vector<vector<int>>& graph)
{
for (int i = 1; graph.size() > i; i++)
{
for (int j = 0; graph[i].size() > j; j++)
{
auto next = graph[i][j];
//현재 정점과 연결된 정점이 같은 색이면 이분 그래프가 아니기 때문에
//즉시 검사를 종료하고 false 리턴
if (visited[i].second == visited[next].second)
return false;
}
}
//모두 다른 색으로 칠해져 있으면 이분 그래프니까 true 리턴
return true;
}
int main()
{
int K;
cin >> K;
for (int i = 0; K > i; i++)
{
int V, E;
cin >> V >> E;
visited.assign(V + 1, make_pair(false, COLORS::NONE));
vector<vector<int>> graph(V + 1);
for (int j = 0; E > j; j++)
{
int from, to;
cin >> from >> to;
graph[from].emplace_back(to);
graph[to].emplace_back(from);
}
for (int i = 1; graph.size() > i; i++)
{
//완전 연결그래프가 아닐 수도 있기 때문에 모든 정점을 방문할 때까지 dfs 반복
if (!visited[i].first)
{
visited[i] = make_pair(true, curColor);
dfs(graph, i);
}
}
//그래프 검사 결과에 따라 정답을 출력한다.
if (isBipartiteGraph(graph))
cout << "YES\n";
else
cout << "NO\n";
}
return 0;
}'알고리즘 문제 풀이 > DFS BFS' 카테고리의 다른 글
| [C++] 백준 온라인 저지 2573번 빙산 풀이 (0) | 2021.11.14 |
|---|---|
| [C++] 프로그래머스 네트워크 풀이 (0) | 2021.11.14 |
| [C++] 백준 온라인 저지 2644번 촌수계산 풀이 (0) | 2021.11.13 |
| [C++] 백준 온라인 저지 1520번 내리막 길 풀이 (0) | 2021.11.10 |
| [C++] 백준 온라인 저지 11725번 트리의 부모 찾기 풀이 (0) | 2021.11.09 |
- Total
- Today
- Yesterday
- 해커랭크
- 기초
- 하드웨어
- 코딩공부
- C언어기초
- hackerrank
- 백준
- 캐나다
- 컴퓨터
- c언어
- dp
- 아이패드
- 다이나믹프로그래밍
- 컴퓨터공부
- 깊이우선탐색
- 문제풀이
- DFS
- greedy
- 애플
- 너비우선탐색
- c++
- 캐나다생활
- 영어공부
- 프로그래밍
- 컴퓨터사이언스
- 알고리즘
- 프로그래머스
- 스위프트플레이그라운드
- 그리디
- BFS
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
